Bdtjtk

O paralelogramo tem área 4, o círculo tem área 94π{displaystyle {frac {9}{4}}pi } e o triângulo tem área 92.{displaystyle {frac {9}{2}}.}

Área é um conceito matemático que pode ser definida como quantidade de espaço bidimensional, ou seja, de superfície.^[1]

Existem várias unidades de medida de área, sendo a mais utilizada o metro quadrado (m²) e os seus múltiplos e sub-múltiplos.^[2] São também muito usadas as medidas agrárias: are, que equivale a cem metros quadrados; e seu múltiplo hectare, que equivale a dez mil metros quadrados. Outras unidades de medida de área são o acre e o alqueire.

Na geografia e cartografia, o termo "área" corresponde à projeção num plano horizontal de uma parte da superfície terrestre. Assim, a superfície de uma montanha poderá ser inclinada, mas a sua área é sempre medida num plano horizontal.

Definição formal |

Uma abordagem para definir o que se entende por área é por meio de axiomas. Por exemplo, pode-se definir área como sendo uma função a de uma coleção M de figuras planas de um tipo especial (denominadas conjuntos mensuráveis) no conjunto dos números reais satisfazendo as seguintes propriedades:

• Para qualquer S em M, a(S) ≥ 0.


• Se S e T estão em M então S ∪ T e S ∩ T também estão e, além disso, a(S∪T) = a(S) + a(T) − a(S∩T).


• Se S e T estão em M e S ⊆ T então T − S está em M e a(T−S) = a(T) − a(S).


• Se um conjunto S está em M e S é congruente a T então T também está em M e a(S) = a(T).


• Todo retângulo R está em M. Se o retângulo tem largura h e altura k então a(R) = hk.


• Seja Q um conjunto limitado entre duas regiões com degraus, S e T. Uma região com degraus é formada a partir de uma união finita de retângulos adjacentes apoiados em uma mesma base, isto é, S ⊆ Q ⊆ T. Se existe um único número c tal que a(S) ≤ c ≤ a(T) para quaisquer regiões step S e T, então a(Q) = c.

Pode ser demonstrado que existe uma tal função área.^[3]

Unidades |

Ver artigo principal: Unidades de área

Um metro quadrado delimitado por tubos de PVC.

Cada unidade de comprimento tem uma unidade de área correspondente, igual à área do quadrado que tem por lado esse comprimento. Desta forma, as áreas podem ser medidas em metros quadrados (²), centímetros quadrados (cm²), milímetros quadrados (mm²), quilómetros quadrados (km²), pés quadrados (ft²), jardas quadradas (yd²), milhas quadradas (mi²), e assim por diante. Algebricamente, estas unidades são os quadrados das unidades de comprimento correspondentes.

A unidade do Sistema Internacional para área é o metro quadrado, que é considerado uma unidade derivada de SI.

Conversões |

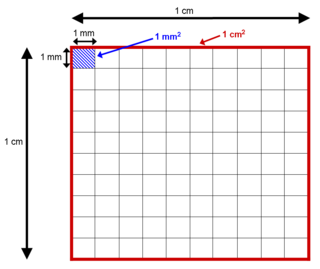
Embora haja 10 mm num cm, há 100 mm² num cm².

A conversão entre duas unidades quadradas é o quadrado do fator de conversão entre as unidades de comprimento correspondentes. Por exemplo, como

1 Pé = 12 polegadas,

é a relação entre pés quadrados e polegadas quadradas, temos que

1 pé = 144 polegadas quadradas,

sendo 144 = 12² = 12 × 12. Da forma análoga:

• 1 quilómetro quadrado = 1 milhão de metros quadrados


• 1 metro quadrado = 10 000 centímetros quadrados = 1 000 000 milímetros quadrados


• 1 centímetro quadrado = 100 milímetros quadrados


• 1 jarda quadrada = 9 pés quadrados


• 1 milha = 3.097.600 jardas quadradas = 27.878.400 pés quadrados

Outras unidades |

Existem várias outras unidades usadas para áreas. O are foi a unidade de medida original do sistema métrico para a área.

• 1 are = 100 metros quadrados

Embora o are tenha caído em desuso, o hectare ainda é muito usado para medir terrenos e propriedades:

• 1 hectare = 100 ares = 10 000 metros quadrados = 0,01 quilómetros quadrados

Outras unidades métricas menos habituais para a área incluem a tétrade, hectade e miríade.

O acre também é muito usado na medição da área de terrenos, sendo

• 1 acre = 4.840 jardas quadradas = 43.560 pés quadrados.

Um acre é aproximadamente 40% de um hectare.

História |

Acredita-se que as necessidades cotidianas, tais como as divisões de terra para o plantio às margens dos rios, a construção de residências, assim como os estudos relativos aos movimentos dos astros inserem-se no contexto de atividades ligadas à geometria e desenvolvidas pelos seres humanos ao longo da evolução humana.

Dentre os principais matemáticos da antiguidade responsáveis pelo desenvolvimento da geometria destacam-se Tales de Mileto (VI a. C.), na Grécia, importando a geometria utilizada pelos egípcios; Pitágoras, conhecido pelo teorema aplicado ao triângulo retângulo que recebeu o seu nome e aperfeiçoou o conceito de demonstração matemática da época. E, ainda nesse século, "os Elementos” de Euclides trouxeram inovações consistentes quanto aos métodos utilizados na antiguidade e que vêm contribuindo há mais de 20 séculos para o desenvolvimento das ciências, baseando-se em três conceitos básicos, tais como ponto, reta e círculo, como também nos cinco postulados. É um sistema axiomático que surge de conceitos e proposições aceitos sem demonstração, conhecidos como, postulados e axiomas.

Uma curiosidade interessante dentro do trabalho com áreas diz respeito ao corpo humano como unidade. Assim, palmos, pés, passos, braças e cúbitos, foram algumas das primeiras unidades de medida utilizadas direta ou indiretamente. Aproximadamente em 3500 a. C., período em que iniciavam-se a construção dos primeiros templos na Mesopotâmia e no Egito, os responsáveis por tais projetos sentiram a necessidade de encontrar unidades de medidas mais regulares e exatas, usaram então como base de medida as partes do corpo de apenas um homem (por exemplo, o rei) e com tais medidas confeccionaram réguas de madeiras e metal, ou ainda com nós, as quais destacaram-se como as primeiras medidas oficiais de comprimento.

O cálculo de áreas iniciou-se possivelmente pela prática da arrecadação de impostos pelos sacerdotes, os quais calculavam intuitivamente a extensão dos campos só pela observação visual, com o tempo observaram trabalhadores revestindo uma parte retangular do chão com pedras quadradas e perceberam que para determinar a quantidade de pedras, seria suficiente contar a quantidade de quadrados de uma fileira e multiplicar pelo número de fileiras existentes, dando origem assim à fórmula para o cálculo da área de um retângulo, sendo esta obtida a partir produto da base pela altura.

Logo após, desenvolveram uma fórmula para o cálculo da área de um triângulo, fundados num pensamento bastante geométrico, no qual tinham a área de um quadrado ou retângulo e dividindo-os ao meio em diagonal obtinham a área do triângulo, assim a área do triângulo é dada pela metade da área do quadrado ou do retângulo. Quando o terreno não tinha a forma retangular ou triangular, os primeiros cartógrafos e agrimensores, utilizavam a triangulação, que consistia num processo de divisão da área em triângulos, cuja soma de suas áreas representava o total da área.

No entanto, esse processo de triangulação apresentava alguns pequenos erros, ao medir a área de terrenos não planos ou com curvas. Surgiu assim a necessidade de calcular o comprimento da circunferência e a área do círculo. Com uma corda pequena ou grande sendo girada em torno de um ponto fixo tinha-se a figura de um circunferência. Essa corda, medida que conhecemos como raio da circunferência, tinha alguma relação com o comprimento da circunferência, assim, tomando essa corda e observando quantas vezes ela caberia na circunferência, perceberam que cabia pouco mais de seis vezes e um quarto, independente do seu tamanho. Desta forma concluíram que o comprimento da circunferência poderia ser dado por 6,28 vezes a medida do raio o que corresponde ao que calculamos hoje quando fazemos C=2πr{displaystyle C=2pi r}, onde π{displaystyle pi } vale aproximadamente 3,14{displaystyle 3,14}.

Quanto à área do círculo, por volta de 2000 anos a.C., conta-se que Ahmes, um escriba egípcio, se propôs a determinar a área de um círculo, pensando inicialmente em calcular a área de um quadrado e obter o número de vezes que essa área caberia na área do círculo. Depois para definir qual seria esse quadrado, considerou mais adequado utilizar o quadrado cujo lado tivesse a mesma medida do raio do círculo do qual se desejava calcular a área, assim procedendo provou que o quadrado se inseria no círculo entre três e quatro vezes, o que representava uma aproximação de três vezes e um sétimo, o que atualmente consideramos aproximado a 3,14 vezes. Desta forma determinou a área do círculo multiplicando a área do quadrado por 3,14, situação que utilizamos atualmente com A=πr2{displaystyle A=pi r^{2}}, com π{displaystyle pi } valendo aproximadamente 3,14{displaystyle 3,14}.

Na Grécia, aproximadamente em 500 a. C. foram fundadas as primeiras universidades. Neste período Tales e seu discípulo Pitágoras organizaram, desenvolveram e aplicaram todo o conhecimento da Babilônia, Etúrria, Egito e Índia à matemática, navegação e religião. Neste período, crescia a curiosidade e a procura por livros de geometria, o conhecimento do Universo ampliava-se velozmente e a escola de Pitágoras fez afirmações quanto à forma da Terra identificando-a como esférica ao invés de plana. Surgiram novas construções geométricas, e suas áreas e perímetros eram agora fáceis de calcular.^[4]

Fórmulas de cálculo |

Retângulo |

Retângulo com área lw.

A mais simples fórmula de cálculo de uma área é a do retângulo
Dado um retângulo com base l e altura w, a sua área é:

A=l×w{displaystyle A=ltimes w} (área do retângulo)^[5]

Ou seja, a área do retângulo é obtida multiplicando a largura pela altura. Um caso particular é a área do quadrado; sendo l o comprimento do seu lado, a sua área é:

A=l2{displaystyle A=l^{2}} (área do quadrado)^[5]

A fórmula para a área do retângulo decorre diretamente das propriedades básicas da área, e por vezes é tomada como uma definição ou axioma.
Tendo a geometria sido desenvolvida antes da aritmética, o conceito de área pode ser usado para definir a multiplicação de números reais.

Dissecção de um paralelogramo.

Fórmulas por dissecção |

A maioria das outras fórmulas simples para o cálculo da área seguem o método da dissecção.
Como o nome indica, este método envolve seccionar a figura em partes mais simples, calcular a área de cada uma dessas partes, que somadas resultarão na área da figura original.

Por exemplo, um paralelogramo pode ser dividido num trapezoide e num triângulo retângulo, como ilustrado pela figura da esquerda.
Se movermos o triângulo para o outro lado do trapezoide, o resultado é um retângulo.
A conclusão é que a área do paralelogramo é igual à do retângulo:

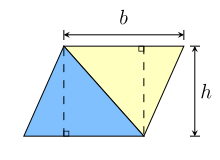
Dois triângulos iguais.

A=b×h{displaystyle A=btimes h} (área do paralelogramo)

O mesmo paralelogramo pode ser dividido em dois triângulos congruentes através de um corte na diagonal, como mostrado na figura da direita:

A=b×h2{displaystyle A={frac {btimes h}{2}}} (área do triângulo)

É possível fazer raciocínios semelhantes para obter fórmulas para as áreas do trapezoide, do losango e de outros polígonos mais complicados.

Área de outros polígonos |

Área do trapézio:

A=B+b2×h{displaystyle A={frac {B+b}{2}}times h} (B = base maior; b = base menor; h = altura)^[6]

Área do losango:

A=D×d2{displaystyle A={frac {Dtimes d}{2}}} (D = diagonal maior; d = diagonal menor)^[7]

Área de qualquer polígono regular:

P×a2{displaystyle {frac {Ptimes a}{2}}} (P = perímetro; a = comprimento do apótema)^[8]

Dividindo o círculo em setores que podem ser rearranjados num paralelogramo aproximado.

Círculo |

A área de um círculo também pode ser calculada através do método de dissecção. Dado um círculo com raio r{displaystyle r} é possível dividi-lo em setores. Cada setor tem uma forma aproximadamente triangular, e os setores podem ser rearranjados para formar uma figura próxima de um paralelogramo. A altura do paralelogramo é r{displaystyle r} e a largura é metade da circunferência do círculo, ou seja, πr.{displaystyle pi r.} Resulta que a área do círculo é r×πr,{displaystyle rtimes pi r,} ou seja, πr2:{displaystyle pi r^{2}:}

A=π×r2{displaystyle A=pi times r^{2}} (área do círculo; r = raio)^[9]

Embora a dissecação usada na fórmula seja aproximada, o erro torna-se cada vez menor à medida que usamos setores cada vez menores.
O limite da área quando o tamanho dos setores tendo para zero é exatamente πr2,{displaystyle pi r^{2},} que corresponde à área do círculo.

Este raciocínio é uma aplicação simples dos conceitos do cálculo. No passado, o método da exaustão foi usado de forma semelhante para encontrar a área do círculo, sendo reconhecido como um precursor do cálculo integral.
Usando os métodos modernos, a área do círculo pode ser calculada usando um integral:

A=∫−rr2r2−x2dx=πr2.{displaystyle A;=;int _{-r}^{r}2{sqrt {r^{2}-x^{2}}},dx;=;pi r^{2}.}

Área de uma superfície |

Arquimedes relacionou a área e volume da esfera com o cilindro.

A maioria das fórmulas para o cálculo da área de uma superfície pode ser obtida cortando e endireitando a superfície.
Por exemplo, a superfície de um cilindro pode ser cortada e estendida formando um retângulo. Da mesma forma, a superfície de um cone pode ser cortada e endireitada num setor de um círculo, para permitir o cálculo da sua área.

O cálculo da área da superfície de uma esfera é mais complexo, pois a curvatura da superfície dificulta a sua projeção num plano direito. Isso acontece com sólidos com curvatura gaussiana diferente de zero.
O primeiro a obter uma fórmula para o cálculo da área de uma esfera foi Arquimedes na sua obra Sobre a Esfera e o Cilindro. Provou que a área e volume da esfera é exatamente 2/3 da área e volume do cilindro que a envolve.
Tal como acontece com a área do círculo, a fórmula para a área da esfera resulta de métodos similares aos do cálculo.

Á área de uma esfera com raio r{displaystyle r} é:

A=4πr2{displaystyle A=4pi r^{2}} (área da esfera)

Lista de fórmulas |

Fórmulas comumente usadas para o cálculo da área

Figura	Formula	Variáveis
Triângulo equilátero	L243{displaystyle {frac {L^{2}}{4}}{sqrt {3}}}	L{displaystyle L} é comprimento de um lado do triângulo.
Triângulo	p(p−a)(p−b)(p−c){displaystyle {sqrt {p(p-a)(p-b)(p-c)}}}	p{displaystyle p} é metade do perímetro, a,{displaystyle a,} b{displaystyle b} e c{displaystyle c} é o comprimento de cada um dos lados.
Triângulo	12absen(C){displaystyle {tfrac {1}{2}}abmathrm {sen} ,(C)}	a{displaystyle a} e b{displaystyle b} são quaisquer dois lados, e C{displaystyle C} é o ângulo entre eles.
Triângulo	12bh{displaystyle {tfrac {1}{2}}bh}	b{displaystyle b} e h{displaystyle h} são a base e altura (medida perpendicularmente à base), respetivamente.
Quadrado	l2{displaystyle l^{2}}	l{displaystyle l} é o comprimento de um dos lados do quadrado.
Retângulo	ab{displaystyle ab}	a{displaystyle a} e b{displaystyle b} são o comprimento de cada um dos lados do retângulo.
Losango	12ab{displaystyle {tfrac {1}{2}}ab}	a{displaystyle a} e b{displaystyle b} são o comprimento de cada uma das diagonais do losango.
Paralelogramo	bh{displaystyle bh}	b{displaystyle b} é o comprimento da base e h{displaystyle h} é a altura medida na perpendicular.
Trapézio	12(a+b)h{displaystyle {tfrac {1}{2}}(a+b)h}	a{displaystyle a} e b{displaystyle b} são os lados paralelos e h{displaystyle h} a distância (altura) entre os lados paralelos.
Hexágono regular	3L223{displaystyle {frac {3L^{2}}{2}}{sqrt {3}}}	L{displaystyle L} é o comprimento de um dos lados do hexágono.
Octógono regular	2(1+2)l2{displaystyle 2(1+{sqrt {2}})l^{2}}	l{displaystyle l} é o comprimento de um dos lados do octógono
Polígono regular	14nl2⋅cot⁡(π/n){displaystyle {frac {1}{4}}nl^{2}cdot cot(pi /n)}	l{displaystyle l} é o comprimento de um dos lados e n{displaystyle n} o número de lados.
Polígono regular	12nR2⋅sen(2π/n)=nr2tan⁡(π/n){displaystyle {frac {1}{2}}nR^{2}cdot mathrm {sen} ,(2pi /n)=nr^{2}tan(pi /n)}	R{displaystyle R} é o raio do círculo circunscrevente, r{displaystyle r} o raio do círculo interior, e n{displaystyle n} é o número de lados.
Polígono regular	12ap{displaystyle {tfrac {1}{2}}ap}	a{displaystyle a} é o apótema (raio do círculo interior ao polígono) e p{displaystyle p} é o perímetro do polígono.
Círculo	πr2 ou πd24{displaystyle pi r^{2} {text{ou}} {frac {pi d^{2}}{4}}}	r{displaystyle r} é o raio e d{displaystyle d} o diâmetro.
Setor circular	12r2θ{displaystyle {tfrac {1}{2}}r^{2}theta }	r{displaystyle r} e θ{displaystyle theta } são, respetivamente, o raio e ângulo (em radianos).
Elipse	πab{displaystyle pi ab}	a{displaystyle a} e b{displaystyle b} são o semieixo maior e semieixo menor, respetivamente.
Área total da superfície do cilindro	2πr(r+h){displaystyle 2pi r(r+h)}	r{displaystyle r} e h{displaystyle h} são o raio e altura do cilindro.
Superfície lateral do cilindro	2πrh{displaystyle 2pi rh}	r{displaystyle r} e h{displaystyle h} são o raio e altura do cilindro.
Superfície total do cone	πr(r+l){displaystyle pi r(r+l)}	r{displaystyle r} e l{displaystyle l} são o raio e a distância do vértice ao círculo base, respetivamente.
Superfície total da esfera	4πr2 ou πd2{displaystyle 4pi r^{2} {text{ou}} pi d^{2}}	r{displaystyle r} e d{displaystyle d} são o raio e o diâmetro, respetivamente.
Superfície total da pirâmide	B+PL2{displaystyle B+{frac {PL}{2}}}	B{displaystyle B} é a área da base, P{displaystyle P} o perímetro da base e L{displaystyle L} a distância do vértice aos cantos da base.

Aplicações |

Pode-se operacionalizar as áreas de algumas figuras planas e utilizá-las em algumas aplicações úteis. Evidentemente, associa-se área de uma figura plana a um número positivo, o qual expressa o espaço do plano ocupado por ela.

Notação |

Usa-se a escrita (ABC...N){displaystyle (ABC...N)} para indicar a área de um polígono de N{displaystyle N} vértices. Vale lembrar que em qualquer polígono o número de vértices é igual ao número de lados.

Área de um triângulo |

Critério para equivalência de triângulos |

Propriedade 1 |

Dois triângulos de mesma base e mesma altura têm áreas iguais.

Demonstração: Dadas duas retas paralelas r{displaystyle r} e s{displaystyle s}, a uma distância d{displaystyle d}, marcamos sobre a reta r{displaystyle r}, os pontos A{displaystyle A} e B{displaystyle B}, e sobre a reta s{displaystyle s}, marcamos os pontos, C{displaystyle C} e C′{displaystyle C^{prime }}, conforme figura abaixo.

Essa é uma consequência do corolário: Sejam ABC{displaystyle ABC} e ABC′{displaystyle ABC^{prime }} triângulos tais que AB//CC′{displaystyle AB//CC^{prime }}. Então (ABC)=(ABC′){displaystyle (ABC)=(ABC^{prime })}.^[10]

Analisando as áreas dos triângulos ABC{displaystyle ABC} e ABC′{displaystyle ABC^{prime }}, temos que:

(ABC)=AB⋅d2{displaystyle (ABC)=ABcdot {frac {d}{2}}}

(ABC′)=AB⋅d2{displaystyle (ABC^{prime })=ABcdot {frac {d}{2}}}

Assim, como r//s{displaystyle r//s} e a distância de r{displaystyle r} a s{displaystyle s} dada por d(r,s)=d{displaystyle d(r,s)=d}, se A{displaystyle A} e B{displaystyle B} pertencem a reta r{displaystyle r} e C{displaystyle C} pertence a reta s{displaystyle s}, obtendo um ponto qualquer C′{displaystyle C^{prime }} sobre a reta s{displaystyle s}, temos AB//CC′{displaystyle AB//CC^{prime }}, portanto os dois triângulos ABC{displaystyle ABC} e ABC′{displaystyle ABC^{prime }} possuem a mesma base AB{displaystyle AB} e a mesma altura d{displaystyle d}, logo suas áreas são iguais.

Propriedade 2 |

Se dois triângulos possuem mesma altura, então a razão entre as suas áreas é igual à razão entre as suas bases.

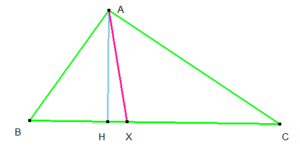
Na triângulo ABC{displaystyle ABC}, foi traçada uma ceviana a partir do vértice A{displaystyle A} intersectando o lado BC{displaystyle BC} no ponto X{displaystyle X}, ficando assim determinados dois triângulos: AXB{displaystyle AXB} e AXC{displaystyle AXC}, de mesma altura AH{displaystyle AH}.

Demonstração: Fazendo a razão entre as áreas temos,

(AXB)(AXC)=12BX⋅AX12CX⋅AH=BXCX{displaystyle {frac {(AXB)}{(AXC)}}={frac {{frac {1}{2}}BXcdot AX}{{frac {1}{2}}CXcdot AH}}={frac {BX}{CX}}}

Portanto,

(AXB)(AXC)=BXCX{displaystyle {frac {(AXB)}{(AXC)}}={frac {BX}{CX}}}

Triângulos semelhantes |

Ver artigo principal: Semelhança de triângulos

Dados dois triângulos semelhantes ABC e MNP, vamos analisar a razão de semelhança entre a razão entre suas áreas e sua razão de semelhança.

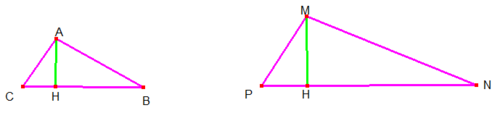
Sejam ABC{displaystyle ABC} e MNP{displaystyle MNP} dois triângulos semelhantes, sendo k{displaystyle k} a razão de semelhança entre seus lados:

MPAC=MNAB=NPBC=k{displaystyle {frac {MP}{AC}}={frac {MN}{AB}}={frac {NP}{BC}}=k}, então temos (MNP)(ABC)=k2{displaystyle {frac {(MNP)}{(ABC)}}=k^{2}}

Demonstração: Como NP=k⋅BC{displaystyle NP=kcdot BC} e HM=k⋅AH{displaystyle HM=kcdot AH}, temos pelas áreas dos triângulos:

(MNP)(ABC)=12NP⋅AM12BC⋅AH=k⋅BC⋅k⋅AHBC⋅AH=k2{displaystyle {frac {(MNP)}{(ABC)}}={frac {{frac {1}{2}}NPcdot AM}{{frac {1}{2}}BCcdot AH}}={frac {kcdot BCcdot kcdot AH}{BCcdot AH}}=k^{2}}

Portanto, dados dois triângulos com razão de semelhança k{displaystyle k} entre seus lados correspondentes, a razão de semelhança entre suas áreas será k2{displaystyle k^{2}}.

A prova do teorema de Pitágoras e outras relações métricas no triângulo retângulo através do cálculo de áreas |

Seja ABC{displaystyle ABC} um triângulo retângulo no vértice A{displaystyle A}, onde a hipotenusa BC=a{displaystyle BC=a}, e seus catetos AB=c{displaystyle AB=c} e AC=b{displaystyle AC=b}, considerando ainda a altura relativa à hipotenusa AH=h{displaystyle AH=h}, bem como as projeções dos catetos sobre a hipotenusa BH=m{displaystyle BH=m} e CH=n{displaystyle CH=n}, temos:

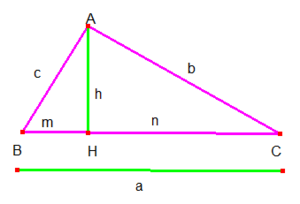
Vamos provar as seguintes relações através do cálculo de áreas:

• I. ah=bc{displaystyle ah=bc}
  


• II. c2=am{displaystyle c^{2}=am} e b2=na{displaystyle b^{2}=na}
  


• III. a2=b2+c2{displaystyle a^{2}=b^{2}+c^{2}}
  

Demonstração I:

I.a) Calculando a área (ABC){displaystyle (ABC)} a partir da base BC{displaystyle BC} e altura AH{displaystyle AH}:

(ABC)=12BC⋅AH=12a⋅h{displaystyle (ABC)={frac {1}{2}}BCcdot AH={frac {1}{2}}acdot h}

I.b) Calculando a área (ABC){displaystyle (ABC)} a partir da base AC{displaystyle AC} e altura AB{displaystyle AB}:

(ABC)=12AC⋅AB=12b⋅c{displaystyle (ABC)={frac {1}{2}}ACcdot AB={frac {1}{2}}bcdot c}

Decorre de I.a) e I.b) temos que (ABC)=12a⋅h=12b⋅c{displaystyle (ABC)={frac {1}{2}}acdot h={frac {1}{2}}bcdot c}.

Logo a⋅h=b⋅c{displaystyle acdot h=bcdot c}

Demonstração II:

II.a) Dado o triângulo ABC{displaystyle ABC}, retângulo em A{displaystyle A}, constrói-se quadrados sobre a hipotenusa BC{displaystyle BC} e os catetos AC{displaystyle AC} e AB{displaystyle AB}, respectivamente de medidas a{displaystyle a}, b{displaystyle b} e c{displaystyle c}. Depois prolonga-se a altura AH{displaystyle AH} até interceptar o lado FG{displaystyle FG} do quadrado BCGF{displaystyle BCGF} no ponto I{displaystyle I}.

Observando os segmentos paralelos BG{displaystyle BG} e AI{displaystyle AI}, percebe-se dois triângulos GBA{displaystyle GBA} e GBH{displaystyle GBH} de mesma área, cujas bases medem a{displaystyle a} e as alturas medem m{displaystyle m}.

Assim, (GBA)=(GBH)=12BG⋅BH=12a⋅m{displaystyle (GBA)=(GBH)={frac {1}{2}}BGcdot BH={frac {1}{2}}acdot m}

Vejamos ainda na figura acima que, os triângulos GBA{displaystyle GBA} e BDC{displaystyle BDC} são congruentes pelo caso LAL, pois BD≡BA{displaystyle BDequiv BA}, BC≡BG{displaystyle BCequiv BG} e ∠CBD≡∠ABC+90∘{displaystyle angle CBDequiv angle ABC+90^{circ }}. Logo, (BDC)=(GBA){displaystyle (BDC)=(GBA)}. E como os segmentos BD{displaystyle BD} e AC{displaystyle AC} são paralelos temos que (BDA)=(BDC){displaystyle (BDA)=(BDC)}, visto que a base BD{displaystyle BD} e a altura AB{displaystyle AB} são comuns aos dois triângulos.

Assim: BD=AB=c{displaystyle BD=AB=c}, então (BDA)=(BDC)=12BD⋅BA=12c⋅c=c22{displaystyle (BDA)=(BDC)={frac {1}{2}}BDcdot BA={frac {1}{2}}ccdot c={frac {c^{2}}{2}}}

Daí, (GBA)=(BDC)⇒am2=c22⇒c2=am{displaystyle (GBA)=(BDC)Rightarrow {frac {am}{2}}={frac {c^{2}}{2}}Rightarrow c^{2}=am}

II.b) De maneira análoga, é provado que b2=an{displaystyle b^{2}=an}

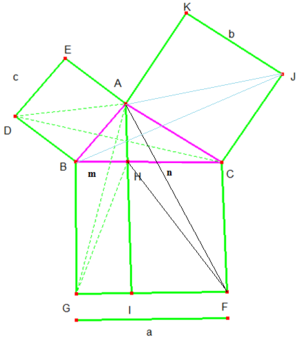
Como AI//CF{displaystyle AI//CF}, temos nos triângulos ACF{displaystyle ACF} e HCF{displaystyle HCF} que (ACF)=(HCF){displaystyle (ACF)=(HCF)}, pois possuem a mesma base CF{displaystyle CF} e mesma altura CH{displaystyle CH}, sendo assim:

(ACF)=(HCF)=12CF⋅CH=12{displaystyle (ACF)=(HCF)={frac {1}{2}}CFcdot CH={frac {1}{2}}}

Temos ainda que os triângulos BCJ{displaystyle BCJ} e ACF{displaystyle ACF} são congruentes pelo caso LAL, pois AC≡CJ=b{displaystyle ACequiv CJ=b}; CF≡BC=a{displaystyle CFequiv BC=a}; ∠ACF≡∠BCJ≡∠ACB+90∘{displaystyle angle ACFequiv angle BCJequiv angle ACB+90^{circ }}. Então, como AK//CJ{displaystyle AK//CJ} temos:

(ACJ)=(BCJ)=12AC⋅CJ=12b2{displaystyle (ACJ)=(BCJ)={frac {1}{2}}ACcdot CJ={frac {1}{2}}b^{2}}

Portanto, da congruência BCJ{displaystyle BCJ} e ACF{displaystyle ACF}, temos:

(BCJ)=(ACF)⇒12b2=12an⇒b2=an{displaystyle (BCJ)=(ACF)Rightarrow {frac {1}{2}}b^{2}={frac {1}{2}}anRightarrow b^{2}=an}

Demonstração III:

De maneira simplificada, somando as duas igualdades II.a) e II.b) temos:

b2=an{displaystyle b^{2}=an} e c2=am{displaystyle c^{2}=am}, logo b2+c2=an+am⇒b2+c2=a(n+m){displaystyle b^{2}+c^{2}=an+amRightarrow b^{2}+c^{2}=a(n+m)}

Como n+m=a{displaystyle n+m=a}, temos:

b2+c2=a(n+m)⇒b2+c2=a2{displaystyle b^{2}+c^{2}=a(n+m)Rightarrow b^{2}+c^{2}=a^{2}} (Teorema de Pitágoras)

Pode-se obter uma demonstração mais elaborada do teorema de Pitágoras por meio do cálculo de áreas. Observando a figura da demonstração II. b) temos que:

BCJ≡ACF{displaystyle BCJequiv ACF}, pelo caso LAL, então (BCJ)=(ACF){displaystyle (BCJ)=(ACF)}. Temos também que (ACJ)=(BCJ)=(ACF){displaystyle (ACJ)=(BCJ)=(ACF)} e (ACF)=(CHF)=(BCJ){displaystyle (ACF)=(CHF)=(BCJ)}. Daí, (ACJ)=(CHF){displaystyle (ACJ)=(CHF)}.

Logo, (ACJK)=2(ACJ)=2(CHF){displaystyle (ACJK)=2(ACJ)=2(CHF)}.

Por outro lado, da demonstração II. b), onde GBA≡BDC{displaystyle GBAequiv BDC}, pelo caso LAL, então (GBA)=(BDC){displaystyle (GBA)=(BDC)}. Temos ainda que (ABD)=(BDC)=(ABG){displaystyle (ABD)=(BDC)=(ABG)} e (ABG)=(BHG)=(BDC){displaystyle (ABG)=(BHG)=(BDC)}. Daí, (ABD)=(BHG){displaystyle (ABD)=(BHG)}.

Logo, (ABDE)=2(ABD)=2(BHG){displaystyle (ABDE)=2(ABD)=2(BHG)}.

Portanto, analisando a área do quadrado BCGF{displaystyle BCGF} de acordo com as demonstrações II. a) e II. b), temos que:

(BCFG)=(CHIF)+(BHGI){displaystyle (BCFG)=(CHIF)+(BHGI)}

(BCFG)=2(CHF)+2(BHG){displaystyle (BCFG)=2(CHF)+2(BHG)}

(BCFG)=(ACJK)+(ABDE){displaystyle (BCFG)=(ACJK)+(ABDE)}

Concluindo, (BCFG)=a2{displaystyle (BCFG)=a^{2}}, (ACJK)=b2{displaystyle (ACJK)=b^{2}} e (ABDE)=c2{displaystyle (ABDE)=c^{2}}

Então, a2=b2+c2{displaystyle a^{2}=b^{2}+c^{2}} (Teorema de Pitágoras)

Área de um trapézio |

No trapézio ABCD{displaystyle ABCD} de altura h{displaystyle h}, temos os lados paralelos AB{displaystyle AB} e DC{displaystyle DC}, tal que
AB=a{displaystyle AB=a} e DC=b{displaystyle DC=b}.

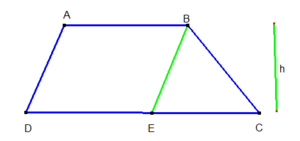
Demonstração: Vamos supor, sem perda de generalidade, que AB>DC{displaystyle AB>DC}, e traçar pelo vértice B{displaystyle B} um segmento paralelo ao lado AD{displaystyle AD} de forma que intercepte o lado DC{displaystyle DC} no ponto E{displaystyle E}.
Assim, como AB//DC{displaystyle AB//DC} e AD//BE{displaystyle AD//BE}, temos o paralelogramo ABED{displaystyle ABED} de altura h{displaystyle h} e base DE=AB=a{displaystyle DE=AB=a}, e temos ainda um triângulo BCE{displaystyle BCE} de base EC=DC−DE=b−a{displaystyle EC=DC-DE=b-a}, e altura h{displaystyle h}.

Note que:

(ABCD)=(ABED)+(BCE)=a⋅h+12(b−a)h=2ah+bh−ah2{displaystyle (ABCD)=(ABED)+(BCE)=acdot h+{frac {1}{2}}(b-a)h={frac {2ah+bh-ah}{2}}}

Portanto,

(ABCD)=(a+b)h2{displaystyle (ABCD)={frac {(a+b)h}{2}}}

Área de um losango |

De acordo com o corolário: Se ABCD é um losango de diagonais AC e BD, então (ABCD)=12ABCD{displaystyle (ABCD)={frac {1}{2}}ABCD}.^[11]

Demonstração: Dado o losango ABCD{displaystyle ABCD}, cujas diagonais interceptam-se no ponto M{displaystyle M}, simultâneamente, ponto médio de ambas as diagonais AC{displaystyle AC} e BD{displaystyle BD}.

Como AB=BC=CD=DA{displaystyle AB=BC=CD=DA}, os triângulos determinados pelas diagonais AC{displaystyle AC} e BD{displaystyle BD}, são isósceles e como M{displaystyle M} é ponto médio destas diagonais, temos que, AM=MC{displaystyle AM=MC}, BM=MD{displaystyle BM=MD}, portanto os triângulos ABD{displaystyle ABD} e BCD{displaystyle BCD} são congruentes pelo caso LAL, assim como os triângulos ADC{displaystyle ADC} e ABC{displaystyle ABC}, pelo mesmo caso.

Sendo assim, vamos mostrar a área do losango através dos triângulos determinados pela diagonal BD{displaystyle BD}.

(ABCD)=(ABD)+(BCD)=12BD⋅MC+12BD⋅AM{displaystyle (ABCD)=(ABD)+(BCD)={frac {1}{2}}BDcdot MC+{frac {1}{2}}BDcdot AM}

(ABCD)=12BD⋅(AM+MC){displaystyle (ABCD)={frac {1}{2}}BDcdot (AM+MC)}.

Como AM+MC=AC{displaystyle AM+MC=AC}, temos:

(ABCD)=12AC⋅BD{displaystyle (ABCD)={frac {1}{2}}ACcdot BD}

Ver também |

• Unidades de área


• Volume

Referências

Ligações externas |

O Commons possui uma categoria contendo imagens e outros ficheiros sobre Área

WikiUnits - Converter Área entre diferentes unidades