Órbita geoestacionária
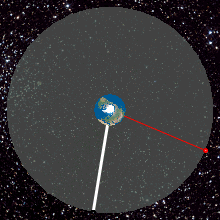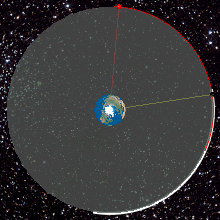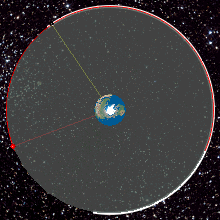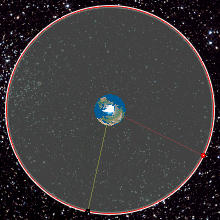
Animação de uma órbita geoestacionária
Uma órbita é considerada geoestacionária quando esta órbita é circular e se processa exatamente sobre o equador da Terra, nos pontos de latitude zero e a sua rotação acompanha exatamente a rotação da Terra.
Desta forma para um observador que estiver situado sobre a superfície, verá que um satélite pertencente a uma órbita geoestacionária, permanece sempre na mesma posição.
É o caso da maioria dos satélites artificiais de comunicações e de televisão que ficam em órbitas geoestacionárias a fim de permanecerem sempre sobre a mesma posição aparente e desta forma sempre poder receber e transmitir dados para uma mesma região o tempo todo. Assim uma antena terrestre pode permanecer fixa apontando sempre uma dada direção do céu, sem necessitar ser redirecionada periodicamente.
Para que um satélite permaneça sempre sobre um determinado ponto da superfície da Terra sem a necessidade de propulsão vertical e horizontal, ele deve orbitar sempre a uma distancia fixa de 35 786 km acima do nível do mar, no plano do equador da Terra. Isso independente da massa do satélite.
Os satélites brasileiros de comunicação da família Brasilsat são satélites de órbita geoestacionária.
Cálculo da altitude de orbitação |
Se um satélite está em orbita em torno da Terra, isso significa que sobre o satélite actua uma força centrípeta (força que a Terra exerce sobre o satélite).
Assim sendo pela Segunda Lei da Dinâmica ou Segunda Lei de Newton temos então a força que atua neste corpo, a força centrípeta:
Fresultante=Fcentrípeta{displaystyle F_{text{resultante}}=F_{text{centrípeta}}}
ou
Fresultante=Fgravitica{displaystyle F_{text{resultante}}=F_{text{gravitica}}}
Pela Segunda Lei de Newton podemos substituir as forças F{displaystyle F} pelas massa do corpo multiplicado por sua aceleração.
Então teremos:
msat⋅ag=msat⋅ac{displaystyle m_{sat}cdot a_{g}=m_{sat}cdot a_{c}}
Observe que a massa do satélite, msat{displaystyle m_{text{sat}}} , aparece em cada lado da igualdade, indicando que podem ser canceladas.
ag=ac{displaystyle a_{g}=a_{c}}
Isso significa que um satélite em órbita geoestacionária não depende de sua massa.
O módulo da aceleração centrípeta é dado por:
|ac|=ω2⋅r{displaystyle |a_{c}|=omega ^{2}cdot r}
Nesta equação ω{displaystyle omega } é a sua velocidade angular e r{displaystyle r} é o raio da órbita, distância esta medida do centro de massa da Terra.
O módulo da aceleração da gravidade, por sua vez, é dado por:
|ag|=Mt⋅Gr2{displaystyle |a_{g}|={frac {M_{text{t}}cdot G}{r^{2}}}}
Nesta equação Mt{displaystyle M_{t}} é a massa da Terra e G{displaystyle G} é a Constante de Gravitação Universal.
G=(6,6742±0,0010)×10−11m3kg−1s−2{displaystyle G=(6,6742pm 0,0010)times 10^{-11}{text{m}}^{3}{text{kg}}^{-1}{text{s}}^{-2}}
Mt=5,9742×1024 kg{displaystyle M_{text{t}}=5,9742times 10^{24} {text{kg}}}
Equacionado-se estas duas acelerações obtemos o seguinte:
ω2⋅r=Mt⋅Gr2{displaystyle omega ^{2}cdot r={frac {M_{t}cdot G}{r^{2}}}}
r3=Mt⋅Gω2{displaystyle r^{3}={frac {M_{text{t}}cdot G}{omega ^{2}}}}
r=Mt⋅Gω23{displaystyle r={sqrt[{3}]{frac {M_{text{t}}cdot G}{omega ^{2}}}}}
Podemos expressar este produto de duas constantes por Mt⋅G{displaystyle M_{text{t}}cdot G} por μ{displaystyle mu }.
r=μω23{displaystyle r={sqrt[{3}]{frac {mu }{omega ^{2}}}}}
A velocidade angular é dada por ω{displaystyle omega } cujo valor é obtido dividindo-se o ângulo percorrido pelo satélite em uma revolução pelo seu período orbital.
O ângulo percorrido vale 360∘=2⋅π{displaystyle 360^{circ }=2cdot pi } radianos.
O tempo que se leva para completar uma revolução de um dia sideral, vale:
86 164 segundos.
Isto fornece:
ω=distânciatempo{displaystyle omega ={frac {text{distância}}{text{tempo}}}}
ω=2⋅π86164=7,29⋅10−5rad⋅s−1{displaystyle omega ={frac {2cdot pi }{86164}}=7,29cdot 10^{-5}mathrm {rad} cdot mathrm {s} ^{-1}}
Temos como resultado que o raio da órbita é 42164 km. Subtraindo-se o raio aproximado da terra que é 6378 km, fornece finalmente a altitude do satélite, que é de 35786 km.
Altitude: 42 164 - 6 378 = 35 786 km
A velocidade orbital (o quanto rápido voa o satélite pelo espaço) é calculado multiplicando-se a velocidade angular pelo raio da órbita.
v=ω⋅r=3,07km⋅s−1{displaystyle v=omega cdot r=3,07mathrm {km} cdot mathrm {s} ^{-1}}
Essas contas devem ser consideradas como uma primeira aproximação: a altitude do satélite deve ser corrigida levando-se em conta a irregularidade da Terra, cujo efeito principal é o do achatamento terrestre.
Ver também |
- Órbita geossíncrona
Ligações externas |
Órbitas Geossíncronas e Geoestacionárias
Descrição do Brasilsat B no site da Boeing (em inglês)
Lista de satélites em órbita geoestacionária (em inglês)
Informações Gerais sobre os Satélites Brasilsat (em português)
Glossário de Astronomia |
Abóbada celeste | |
















![{displaystyle r={sqrt[{3}]{frac {M_{text{t}}cdot G}{omega ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7bb8dffaeac473bb409aa16316d60de9c595b46)


![{displaystyle r={sqrt[{3}]{frac {mu }{omega ^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86fc9c7797f74da609ad17740a92d557e33af69e)



